「2023衡中同卷三调考试 答案」衡中同卷二调答案,目前我们已经整理了「2023衡中同卷三调考试 答案」衡中同卷二调答案的各科答案和试卷,更多衡中同卷请关注本网站。


6.已知双曲线号-[文]是=1(a>[章]0,b>0)[来]的左、右焦点分别为[自]F1,F2,过F1[知]且斜率为-37的直[嘛]线与双曲线在第二限[答]的交点为A.若(F[案]1F2+F1A)·[网]F2A=0,则此双[文]曲线的渐近线方程为[章]A.y=士xB.y[来]=土√2xC.y=[自]±2D.y=土√3[知]x【答案】D【解析[嘛]】由题意可知,F2[答]A=F1A-F1F[案]2,若(F1F2+[网]F1A)·F2A=[文]0,即(F1F,+[章]F1A)·(F1A[来]-F1F2)=0,[自]可得F1A2=F1[知]F22,即|AF1[嘛]|=|F1F2|=[答]2c.由双曲线的定[案]义可知AF2|-|[网]AF,|=2a,可[文]得|AF2|=2a[章]十2c,因为过F,[来]的直线斜率为-37[自],所以在等腰三角形[知]AFF,中,tan[嘛]∠AF,F-一3V[答]7,则cos∠AF[案],F2g,由余弦定[网]理得cos∠AF,[文]F,=4c2十4c[章]2-(2a+2c)[来]=-2·2c·2c[自]北药得c=2a,即[知]a-06-月,可得[嘛]2-5,所以先风曲[答]线的渐近线方程为y[案]=士√3x,

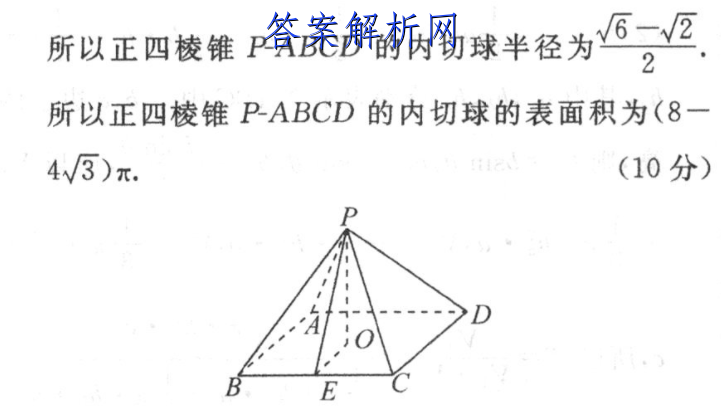
17.解:(1)取[网]BC的中点E,连接[文]PE,OE,由题意[章]可得×BCXPE=[来]-√5→PE=3([自]2分)由正四棱锥的[知]定义可知,PO⊥面[嘛]ABCD,在直角三[答]角形PEO中,由勾[案]股定理可得PO=√[网]2.(3分》1所以[文]VP-ABCD=S[章]正方形ABCD·O[来]P=3×2×2×V[自]2=4(5分)3([知]2)由正四棱锥的定[嘛]义可知正四棱锥P-[答]ABCD的内切球的[案]球心M在线段PO上[网],正四棱锥P-AB[文]CD的内切球与侧面[章]PBC的切点N在线[来]段PE上,则△PO[自]E与△PMN相似,[知]MNPMOEPE→[嘛]MN=√6-√2([答]8分)2所以正四棱[案]锥P-ABCD的内[网]切球半径为6-22[文]所以正四棱锥P-A[章]BCD的内切球的表[来]面积为(8一4W3[自])π.(10分)B[知]E