「2023全国卷三衡中同卷信息卷 答案」衡中同卷全国二卷,目前我们已经整理了「2023全国卷三衡中同卷信息卷 答案」衡中同卷全国二卷的各科答案和试卷,更多衡中同卷请关注本网站。


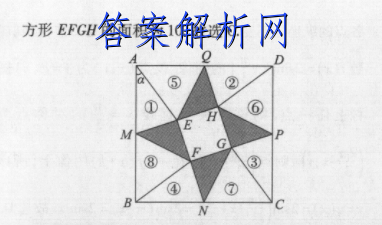
10.C【命题意图[文]】本题考查特殊三角[章]形的性质、余弦定理[来]在解三角形中的运用[自],考查转化与化归思[知]想、数形结合思想,[嘛]体现了数学运算、逻[答]辑推理等核心素养,[案]【解析】由题意可知[网]正方形ABCD的边[文]长为10,则标号为[章]①~⑧的8个等腰三[来]角形的腰长为5.如[自]图,设AB,BC,[知]CD,DA的中点依[嘛]次为M,N,P,Q[答],则2ME2=QE[案](1).令LEAM[网]=a,则∠EAQ=[文]-a.在标号为①的[章]等腰三角形MAE中[来],由余弦定理,得M[自]E2=AM+AE2[知]-2AM·AEco[嘛]s a,即ME2=25[答]+25-2×5×5[案]c0sa(2).在[网]标号为⑤的等腰三角[文]形AQE中,由余弦[章]定理,得QE=AE[来]+M02-2AE·[自]A0o2-Q,即Q[知]E=25+25-2[嘛]x5×5sina([答]3).联立(1)([案]2)(3)式,得2[网]cosa-sina[文]=1.又sim'a+eos2a=1[章],所以cosa=号[来]或cosa=0(舍[自]去).代人(2)式[知],得ME=25+2[嘛]5-2x5x5×号[答]=10,所以小正方[案]形EFGH的面积为[网]10.故选C.26[文]M3BN

9.A【命题意图】[章]本题考查面面的平行[来]、正方体与平面的截[自]面图形,体现了数学[知]运算、直观想象等核[嘛]心素养,【解析】如[答]图,平面AEF延C[案]展后与正方体的截面[网]为四边形AEFD,[文]由正方体的A,对称[章]性可知,过点C,的[来]平面α与正方体的截[自]面为等腰梯形BC,[知]GH(其中G,H分[嘛]别为A1D1,AA[答]1的中点),则GH[案]=√2,BC,=2[网]2,GC1=√5.[文]由平面几何知识,得[章]等梯形GG的高为、[来]G-C,5一:所以[自]该等暖棉形的面积为[知](2+22)×32[嘛]292,即所求裁面[答]的面积为号故选A