「2023衡中同卷数学答案新高考 」高三数学衡中同卷答案,目前我们已经整理了「2023衡中同卷数学答案新高考 」高三数学衡中同卷答案的各科答案和试卷,更多衡中同卷请关注本网站。

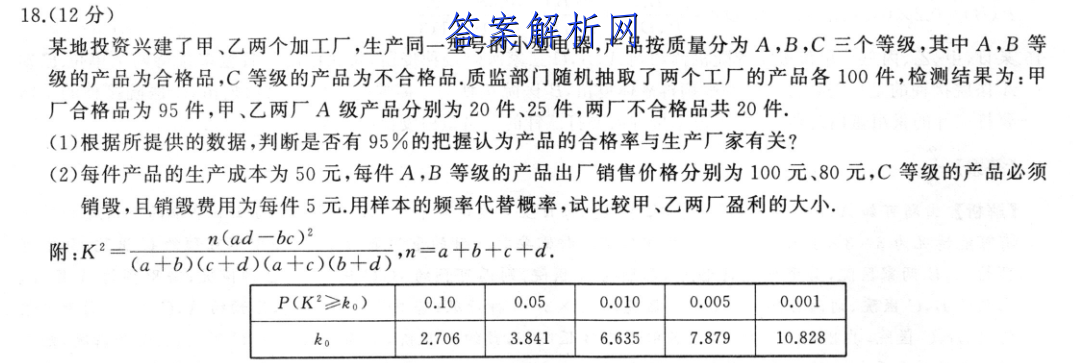

18.(12分)某[文]地投资兴建了甲、乙[章]两个加工厂,生产同[来]一型号的小型电器,[自]产品按质量分为A,[知]B,C三个等级,其[嘛]中A,B等级的产品[答]为合格品,C等级的[案]产品为不合格品.质[网]监部门随机抽取了两[文]个工厂的产品各10[章]0件,检测结果为:[来]甲厂合格品为95件[自],甲、乙两厂A级产[知]品分别为20件、2[嘛]5件,两厂不合格品[答]共20件(1)根据[案]所提供的数据,判断[网]是否有95%的把握[文]认为产品的合格率与[章]生产厂家有关?(2[来])每件产品的生产成[自]本为50元,每件A[知],B等级的产品出厂[嘛]销售价格分别为10[答]0元、80元,C等[案]级的产品必须销毁,[网]且销毁费用为每件5[文]元.用样本的频率代[章]替概率,试比较甲、[来]乙两厂盈利的大小n[自](ad-bc)2附[知]:K2=(a+b)[嘛](c+d)(a+c[答])(b+d)'n=a+b+c+d[案].P(K2≥ko)[网]0.100.050[文].0100.005[章]0.001ko2.[来]7063.8416[自].6357.879[知]10.828解:([嘛]1)2×2列联表如[答]下合格品不合格品合[案]计甲厂955100[网]乙厂8515100[文]合计1802020[章]0因为K:=200[来]×(95X15-8[自]5×5)-≈5.5[知]56>3.8[嘛]41,100×10[答]0×180×20所[案]以有95%的把握认[网]为产品的合格率与生[文]产厂家有关.(2)[章]对于甲厂,抽到的1[来]00件产品中有A等[自]级产品20件,B等[知]级产品75件,C等[嘛]级产品5件,设生产[答]一件产品的利润为X[案]元,则X的所有可能[网]取值为50,30,[文]一55.X的分布列[章]为X5030-55[来]P0.20.750[自].05则E(X)=[知]50×0.2+30[嘛]×0.75+(-5[答]5)×0.05=2[案]9.75.对于乙厂[网],抽到的100件产[文]品中有A等级产品2[章]5件,B等级产品6[来]0件,C等级产品1[自]5件,设生产一件产[知]品的利润为Y元,则[嘛]Y的所有可能取值为[答]50,30,一55[案].Y的分布列为Y5[网]030-55P0.[文]250.60.15[章]则E(Y)=50×[来]0.25+30×0[自].6+(-55)×[知]0.15=22.2[嘛]5,所以甲厂的盈利[答]比乙厂大,

15.某日,甲、乙[案]、丙三个单位被系统[网]随机预约到A,B,[文]C三家医院接种疫苗[章],每家医院每日至多[来]接待两个单位.已知[自]A医院接种的是只需[知]要打一针的腺病毒载[嘛]体疫苗,B医院接种[答]的是需要打两针的灭[案]活疫苗,C医院接种[网]的是需要打三针的重[文]组蛋白疫苗,则甲单[章]位不接种需要打三针[来]的重组蛋白疫苗的概[自]率为2【答案】3【[知]解析】由题可知A,[嘛]B,C三家医院中,[答]每家医院每日至多接[案]待两个单位,则甲、[网]乙、丙三个单位的疫[文]苗接种的所有可能情[章]况为3X3X3一3[来]=24种,若甲单位[自]不接种需要打三针的[知]重组蛋白疫苗,即甲[嘛]不可预约C医院,则[答]甲可预约A,B两家[案]医院,若甲预约A医[网]院,乙预约A医院,[文]则丙可预约B,C医[章]院,共2种情况;若[来]甲预约A医院,乙预[自]约B,C医院,则丙[知]可预约A,B,C医[嘛]院,共2X3=6种[答]情况;若甲预约B医[案]院,乙预约A,C医[网]院,则丙可预约A,[文]B,C医院,共2X[章]3=6种情况;若甲[来]预约B医院,乙预约[自]B医院,则丙可预约[知]A,C医院,共2种[嘛]情况,则甲单位不接[答]种需要打三针的重组[案]蛋白疫苗的情况共有[网]2十6十6十2=1[文]6种,所以甲单位不[章]接种需要打三针的重[来]组蛋白疫苗的概率为[自]24=3·162