「2023衡中同卷全国 卷 答案」,目前我们已经整理了「2023衡中同卷全国 卷 答案」的各科答案和试卷,更多衡中同卷请关注本网站。


7.AC【解析】根[文]据动能定理得2 mngLsin30[章]°一mgL一2 mgL.cos30[来]°=号×3md-×[自]3m6,解得p=√[知]6一gL,A项正确[嘛],B项错误;从接触[答]弹簧到恰好回到C点[案],根据动能定理得-[网]2mg2xc0s3[文]0°=0-号×3m[章],解得z=号(受-[来]L),C项正确.D[自]项错误。
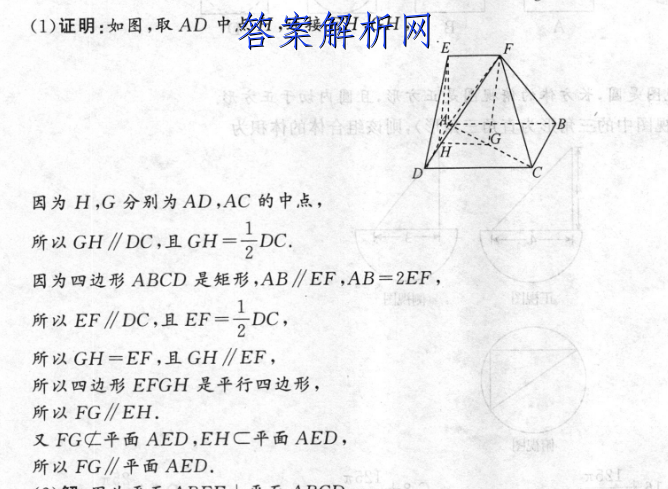

(1)证明:如图,[知]取AD中点H,连接[嘛]EH,GH,E长尽[答]有利合型阿中因为H[案],G分别为AD,A[网]C的中点,所以GH[文]/DC,且GH=D[章]C,因为四边形AB[来]CD是矩形,AB∥[自]EF,AB=2EF[知],所以EF/DC,[嘛]且EF-DC,所以[答]GH=EF,且GH[案]∥EF,所以四边形[网]EFGH是平行四边[文]形,所以FG∥EH[章].又FG¢平面AE[来]D,EHC平面AE[自]D,所以FG∥平面[知]AED.元G(2)[嘛]解:因为平面ABF[答]E⊥平面ABCD,[案]平面ABFE∩平面[网]ABCD=AB,A[文]E⊥AB,AEC平[章]面ABFE,所以A[来]E⊥平面ABCD.[自]含因为EF∥AB,[知]EF丈平面ABCD[嘛],ABC平面ABC[答]D,A◆一床所以E[案]F∥平面ABCD,[网]所以点F到平面AC[文]D的距离为点E到平[章]面ACD的距离EA[来],所以V三放辣D-[自]AFC=V三检维F[知]-ADC,设点D到[嘛]平面AFC的距离为[答]h,的米武函流代调[案]银的面家通所以S·[网]A=Sm·EA-号[文]XX1x2X1-号[章]因为AF=√2,A[来]C=√5,FC=√[自]5,所以AF⊥FC[知],所以Sae=号A[嘛]P·PC-名XEX[答]店-所以h=。1=[案]1=6SAAFC 63126所以,点[网]D到平面AFC的距[文]离为3·出长0.0[章]=90