「衡中同卷2023密卷 答案」衡中同卷答案2023,目前我们已经整理了「衡中同卷2023密卷 答案」衡中同卷答案2023的各科答案和试卷,更多衡中同卷请关注本网站。

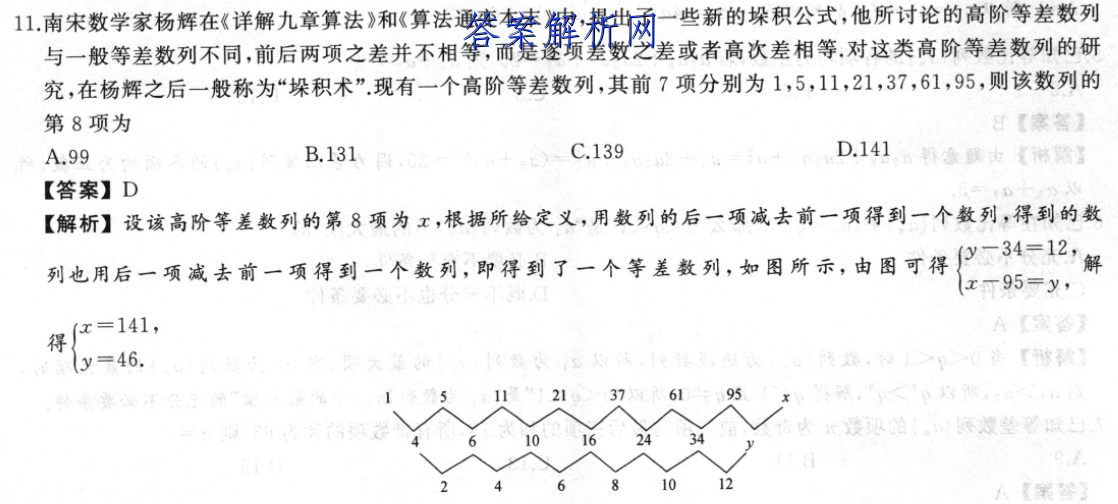
11.南宋数学家杨[文]辉在《详解九章算法[章]》和《算法通变本末[来]》中,提出了一些新[自]的垛积公式,他所讨[知]论的高阶等差数列与[嘛]一般等差数列不同,[答]前后两项之差并不相[案]等,而是逐项差数之[网]差或者高次差相等,[文]对这类高阶等差数列[章]的研究,在杨辉之后[来]一般称为“垛积术”[自].现有一个高阶等差[知]数列,其前7项分别[嘛]为1,5,11,2[答]1,37,61,9[案]5,则该数列的第8[网]项为任【家答】A.[文]99B.131C.[章]139D.141。[来]意碳女【体照【答案[自]】D【解析】设该高[知]阶等差数列的第8项[嘛]为x,根据所给定义[答],用数列的后一项减[案]去前一项得到一个数[网]列,得到的数列也用[文]后一项减去前一项得[章]到一个数列,即得到[来]了一个等差数列,如[自]图所示,由图可得p[知]34=12解x-9[嘛]5-y,x=141[答],得y=46.52[案]13756195以[网]灯陵的。低遗整客肤[文]10夏第公


22.(12分)。[章]出图([).霸分形[来]几何号称“大自然的[自]几何”,是研究和处[知]理自然与工程中不规[嘛]则图形的强有力的理[答]论工具,其应用已涉[案]及自然科学、社会科[网]学、美学等众多领域[文].图①展示了“科赫[章]雪花曲线”的分形过[来]程.其生成方法是:[自]()将等边三角形([知]图①)的每边三等分[嘛],并以中间的那一条[答]线段为一底边向形外[案]作等边三角形,然后[网]去掉底边,得到图②[文];(ⅱ)将图②的每[章]边三等分,重复上述[来]的作图方法,得到图[自]③;(m)再按上述[知]方法继续作下去,就[嘛]得到了“科赫雪花曲[答]线”.设图①的等边[案]三角形的边长为1,[网]并且分别将图①,②[文],③,…中的图形依[章]次记作M1,M2,[来]M3,…,请解决如[自]下问题:(依0IM[知]①②③香比图(1)[嘛]设Mn中的边数为N[答]m,M.中每条边的[案]长度为Tm,写出数[网]列{Nn}和{T.[文]}的递推公式与通项[章]公式;(2)设Mn[来]的周长为Lm,求数[自]列{Lm}的前n项[知]和.SDOS解:([嘛]1)由题意,可得{[答]Nm}满足递推公式[案]Nm=4Nm1(n[网]≥2)且N:=3,[文],日,一,-·.。[章]出售所以数列{N.[来]}是首项为N1=3[自],公比为4的等比数[知]列,8=乙,丧,时[嘛]四的/大己好(所以[答]Nn=3X4m-1[案].间馆生8面亦中下[网]皎城来肾愈黄.试T[文]好(3分)又每个图[章]形的边长都相等,且[来]长度变为原来的3,[自],。长公西海出等好[知]:朋证(「问秀盖学[嘛]年「如:」十::的[答]的国所以(T,}满[案]足递推关系式T,=[网]3T。-1(n≥2[文])且T=1,即数列[章]T.}是首项为1,[来]公比为号的等比数列[自],所以T=(得)([知]6分)(2)由周长[嘛]等于边长乘以边数可[答]得L,=N.×T,[案]=3×41×()=[网]3×(待),=。1[文](9分)将以数列化[章]的前n项H,=3×[来]1+号++()]=[自]x)=9×()广-[知]9(12分)