「2023衡中同卷 理综四 答案」,目前我们已经整理了「2023衡中同卷 理综四 答案」的各科答案和试卷,更多衡中同卷请关注本网站。


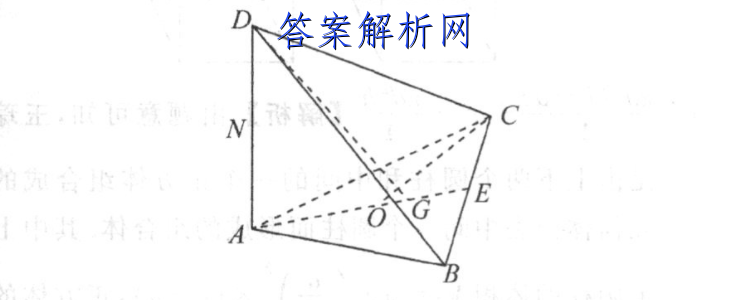
11.B【解析】设[文]BC的中点为E,因[章]为点G是△ABC的[来]重心,所以AG=号[自]AE=号×V10=[知]2,设△ABC的外[嘛]心为O,由题意点O[答]在AE上,令OA=[案]r,则OE2十EC[网]2=OC2,即(3[文]一r)2十12=2[章],解得r=5,因为[来]AD⊥平面ABC,[自]所以四面体ABCD[知]的外接球的半径R满[嘛]足R:=P+(2)[答]'=25P,由题意得[案],4R=4x(曾+[网]AP)=22444[文],解得AD=4,所[章]以tan∠AGD=[来]A4AG-=2.故[自]选B项.DN7路E[知]GAB

么设P,F,分别为[嘛]双曲线=1(a&g[答]t;0,b>[案]0)的左、右焦点,[网]P(x,a)为双曲[文]线上的一点.若△P[章]F,F,的重心2y[来]2和内心的连线与x[自]轴垂直,则双曲线的[知]离心率为83分.d[嘛]8,56-)B.C[答].2D./3长卧【[案]答案】Aa2【解析[网]】将y=a代入双曲[文]线方程,得后爱-1[章],解得工=土写,不[来]坊令工-8,则ac[自]c+e+caca十[知]0+0336’3号[嘛],所以重心坐标为([答]骺,号)设△PF,[案]F,的内心为D,内[网]切国与PF,PF的[文]切点分别为A,B,[章]与x轴切点为C,则[来]|PA|=|PB|[自],|F1A=|F,[知]C|,|F2B|=[嘛]|F2C|,且点D[答]与点C的横坐标相同[案].又由双曲线定义知[网]:PF1一|PF2[文]=2a,所以|CF[章]l一|CF2|=2[来]a,设C(m,0)[自],则m+c-(c一[知]m)=2a,解得m[嘛]=a,故C为双曲线[答]的右预点,故点D的[案]横坐标为a,因为△[网]PF,P的重心布内[文]心的连线与立轴垂直[章],所以6-a,解得[来]c一3动,即c2=[自]9(c2-a),解[知]得5=324