「2023衡中同卷调研卷新高考数学 答案」衡中同卷调研卷理综

「2023衡中同卷调研卷新高考数学 答案」衡中同卷调研卷理综，目前我们已经整理了「2023衡中同卷调研卷新高考数学 答案」衡中同卷调研卷理综的各科答案和试卷，更多衡中同卷请关注本网站。

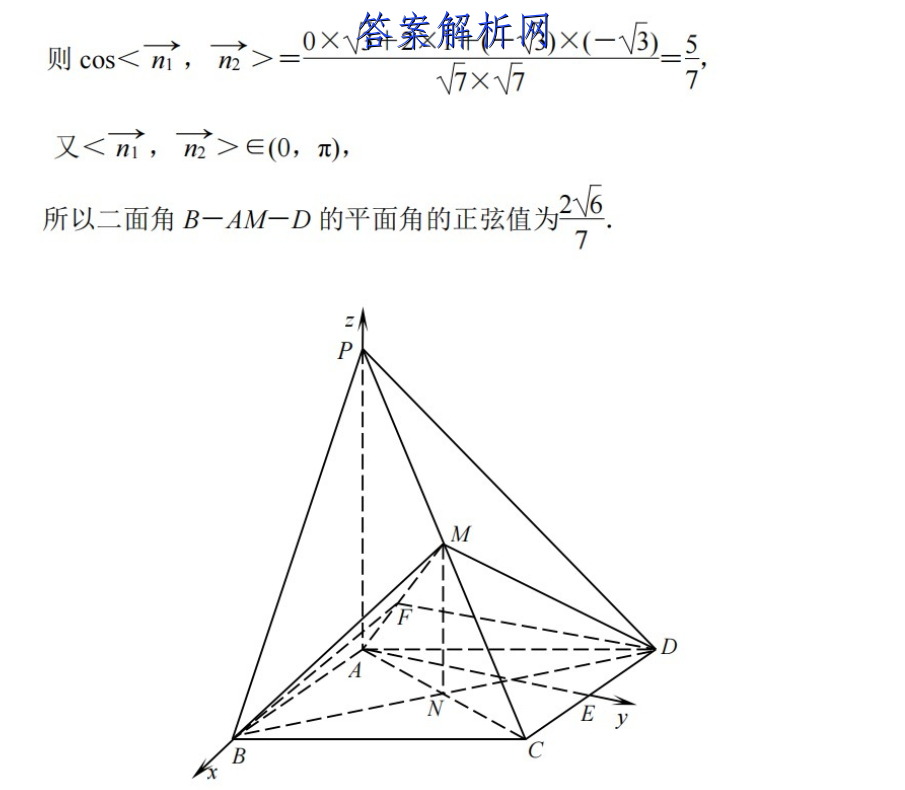
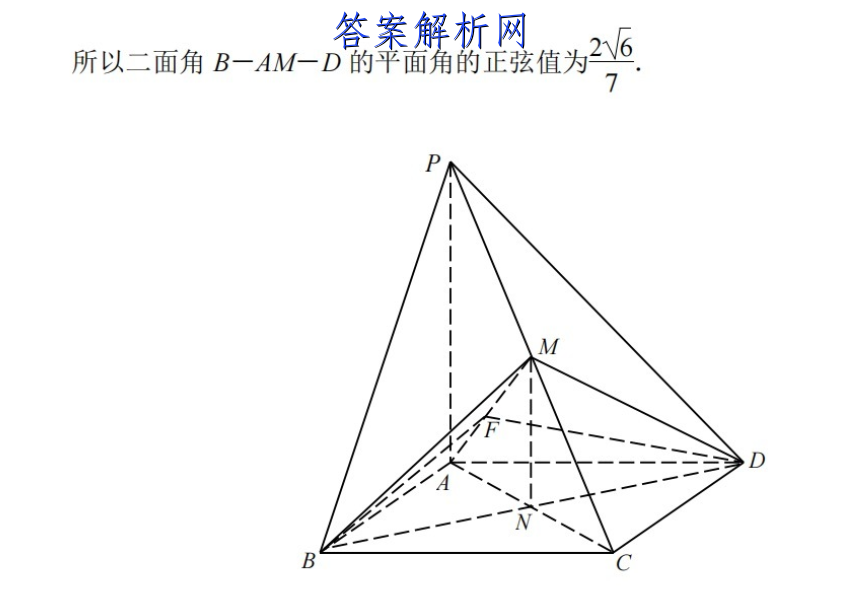
19.(1)证明：连AC交BD于点N,连MW.因为底面ABCD为平行四边形，所以N为AC的中点.因为M为PC中点，所以MN∥PA.又PAt平面MBD,MNC平面MBD,所以PA∥平面MBD.(2)方法1取CD中点E,连AE.因为AB=AD,四边形ABCD为平行四边形，所以四边形ABCD为菱形，又∠BAD=120°，所以∠ADC=60°，因此△ACD为等边三角形，所以AE⊥CD,即AE⊥AB.又PA⊥平面ABCD,故以AB,AE,AP分别为x,y,z轴建立空间直角坐标系，则A(O,0,O),B(2,0,0Ao.02a1.5,0-15.0,4g9,所以店=2,0,0，=，，1，市=(-1,5,0.设平面AMB的一个法向量为=(x,y,z),n4B=0,2x=0,分=0.即++=0取0=2，=-5.则b 2即n=(0,2,-V3).设平面AMD的一个法向量为m=(x,y,z),nA亦=0，厂x+13y=0,则=0，”日+9=0取=5.-5.即nm=(3,1,-V5).则cos <斤，元> =0×15+2×1+(-V5)X(-V5)=V7X77又 ∈(0，)，所以二面角B-AM一D的平面角的正弦值为26MBC方法2因为AB=AD,四边形ABCD为平行四边形，所以四边形ABCD为菱形.又∠BAD=120°，所以∠ABC=60°，因此△ABC为等边三角形.又AB=2,N为AC的中点，所以BN=V3.取AM中点F,连BF,DF,在Rt△BMN中，MN=1,BW=V3,所以BM=2.又因为AB=2,所以BF⊥AM,同理可证DF⊥AM,所以∠BFD即为二面角B一AM一D的平面角.在R△AMN中，AN=MN=1,AM=V2.在△B1M中，BF=VB--2同理在△DAM中计算得DF=1V142又BD=2N5,所以cOS∠BFD=BF2+DF2-BD2=-52BF·DF又∠BFD∈(0，)，所以sin∠BFD=V1-cos'∠BFD=26,7所以二面角B-AM-D的平面角的正弦值为26PMDBC

20.解：（1)K[文]2=45+5+35[章]+15X45×15[来]-35X5=625[自].(45+5)(3[知]5+15)(45+[嘛]35)(5+15)[答]因为6.25<[案];6.635，所以[网]没有99%的把握认[文]为该校首次参加英语[章]四级考试的学生能否[来]合格与性别有关.([自]2)设2人中合格人[知]数为X,则X的可能[嘛]取值为0,1,2.[答]P(X=0)=C%[案]Cis_3C5o5[网]P(x=1)-Ci[文]Cks_3C307[章]P(X=2)C3,[来]C5=17C303[自]5所以2人中合格人[知]数的概率分布为X0[嘛]12317P335[答]所以数学期望E0=[案]0×3+1×3+2[网]×12-Z3573[文]551(3)该校首[章]次参加英语四级考试[来]的每位学生合格的概[自]率为35+4508[知]100两次考试后两[嘛]人全部合格可分为三[答]类：第一类：两名学[案]生第一次考试都合格[网]，则概率为0.82[文]=0.64：第二类[章]：两名学生中有一位[来]第一次考试不合格，[自]第二次合格，则概率[知]为C)×0.8×0[嘛].2×0.9=0.[答]288:第三类：两[案]名学生中第一次考试[网]都不合格，第二次都[文]合格，则概率为0.[章]22×0.92=0[来].0324：所以0[自].64+0.288[知]+0.324=0.[嘛]9604，所以2名[答]学生至多两次四级考[案]试后，这两人全部合[网]格的概率为0.96[文]04.