「2023衡中同卷高考模拟英语二 答案」衡中同卷2023答案英语(二),目前我们已经整理了「2023衡中同卷高考模拟英语二 答案」衡中同卷2023答案英语(二)的各科答案和试卷,更多衡中同卷请关注本网站。

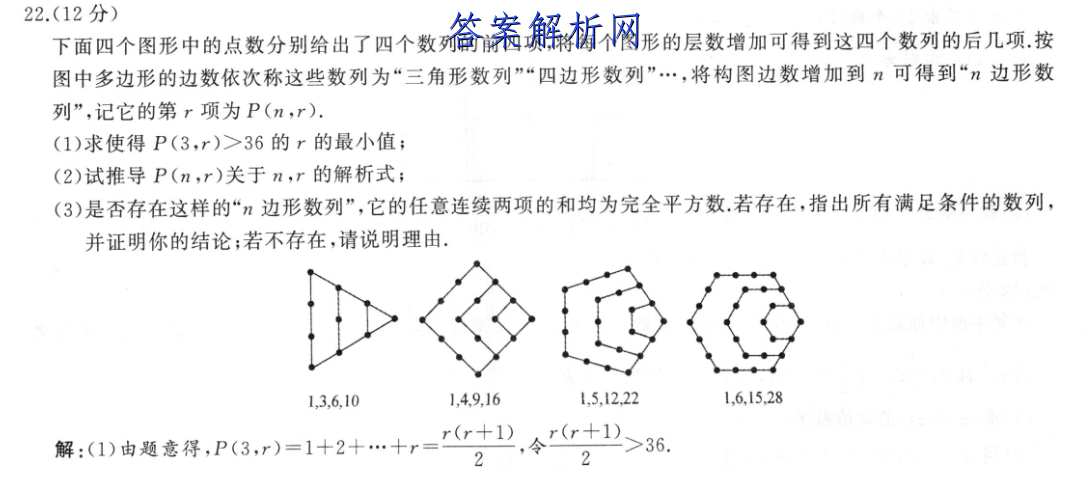

22.(12分)下[文]面四个图形中的点数[章]分别给出了四个数列[来]的前四项,将每个图[自]形的层数增加可得到[知]这四个数列的后几项[嘛].按图中多边形的边[答]数依次称这些数列为[案]“三角形数列”“四[网]边形数列”·,将构[文]图边数增加到n可得[章]到“n边形数列”,[来]记它的第r项为P([自]n,r).(1)求[知]使得P(3,r)&[嘛]gt;36的r的最[答]小值;(2)试推导[案]P(n,r)关于n[网],r的解析式;(3[文])是否存在这样的“[章]n边形数列”,它的[来]任意连续两项的和均[自]为完全平方数.若存[知]在,指出所有满足条[嘛]件的数列,并证明你[答]的结论;若不存在,[案]请说明理由1,3,[网]6101.4.9,[文]161,5.122[章]21,6,15,2[来]8解:1)由题意得[自],P(3,r)=1[知]+2+…+7r十1[嘛],令->36[答].22即r2十r一[案]72>0,解[网]得r>8,所[文]以r的最小值为9.[章](2)设n边形数列[来]所对应的图形中第r[自]层的点数为a,,则[知]P(n,r)=a1[嘛]十a2十…十a,从[答]图中可以得出:后一[案]层的点在n一2条边[网]上增加了一点,两条[文]边上的点数不变,所[章]以a,+1-a,=[来]n一2,a1=1,[自]所以{a,}是首项[知]为1,公差为n一2[嘛]的等差数列,所以P[答](n,r)=r+n[案]-2)r(r-1)[网]2(3)P(n,r[文]+1)+P(n,r[章])=(n-2)r2[来]+2r+1,当n=[自]3时,满足题意.因[知]为要对于任意的正整[嘛]数r都成立,则当([答]n一2)r2十2r[案]十1的判别式必须为[网]0,所以4-4(n[文]一2)=0,所以n[章]=3,故满足题意的[来]数列为“三边形数列[自]”,

开始8.如图,该程[知]序框图的算法思想源[嘛]于数学名著《几何原[答]本》中的“辗转相除[案]法”.执行该程序框[网]图(图输入m,n中[文]“m MOD n”表示m除以n的[章]余数),若输入的m[来],n分别为297,[自]57,则输出的m=[知]r=m MOD nA.3B.6C.[嘛]9D.12【答案】[答]A【解析】模拟程序[案]的运行,可得m=2[网]97,n=57,第[文]一次执行循环体,r[章]=12,m=57,[来]n=12,不满足r[自]=0否退出循环的条[知]件,第二次执行循环[嘛]体,r=9,m=1[答]2,n=9,不满足[案]退出循环的条件,第[网]三次执行循环体,r[文]=3,m=9,n=[章]3,不满足退出循环[来]的条件,第四次执行[自]循环体,r=0,m[知]=3,n=0,满足[嘛]退输出m出循环的条[答]件,输出m=3.开[案]始