「衡中同卷2023版理数 答案」衡中同卷2023版答案,目前我们已经整理了「衡中同卷2023版理数 答案」衡中同卷2023版答案的各科答案和试卷,更多衡中同卷请关注本网站。


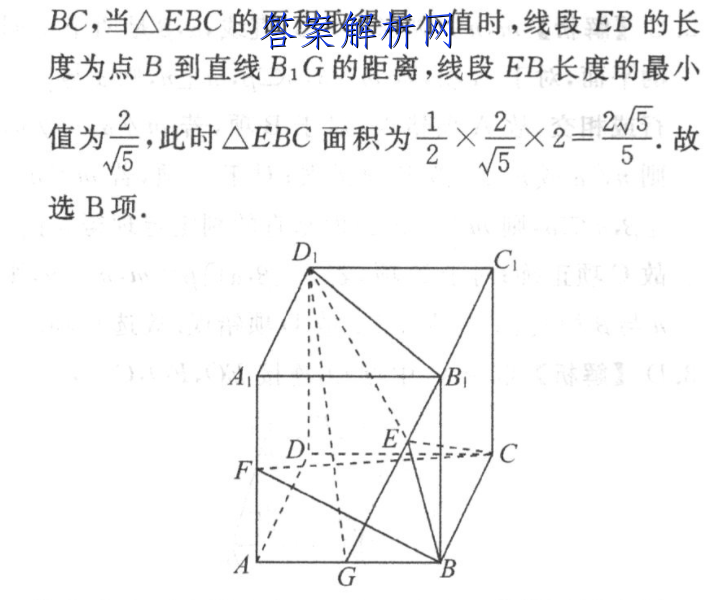
11.B【解析】如[文]图,取AB中点G,[章]可知Rt△BAF≌[来]Rt△B1BG,得[自]∠ABF=∠BB1[知]G,所以∠B,GB[嘛]+∠ABF=∠B1[答]GB+∠BB1G=[案]90°,所以BF⊥[网]B1G.又因为B1[文]G⊥BC,BC∩B[章]F=B,所以B1G[来]⊥平面BFC,所以[自]B1G⊥CF,又因[知]为D1E⊥CF,B[嘛]1G∩D1E=E,[答]所以CF⊥平面B1[案]DG,当点E在直线[网]B,G上时,D1E[文]⊥CF,BC=2,[章]则△BCE面积为E[来]BBC,当△EBC[自]的面积取得最小值时[知],线段EB的长度为[嘛]点B到直线B,G的[答]距离,线段EB长度[案]的最小做为后,此时[网]△BC面积为号×后[文]×=2故选B项.A[章]BDEF:AiCB[来]

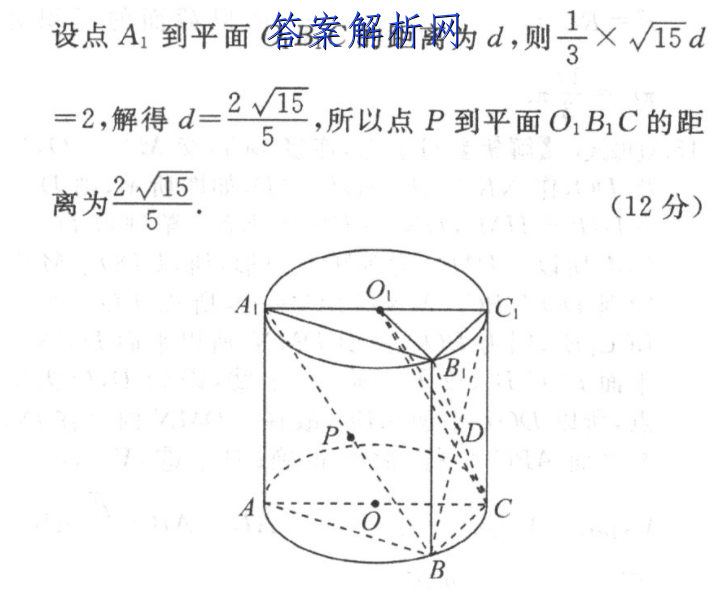
21.(1)证明:[自]连接BC1交B1C[知]于点D,连接O1D[嘛],由题意可得,四边[答]形BCCB1为平行[案]四边形,则点D为B[网]C1的中点.(2分[文])又点O1为A1C[章]1的中点,所以O1[来]D∥A1B.(3分[自])因为O1DC平面[知]O1B1C,A1B[嘛]¢平面O1B1C,[答]所以A1B∥平面O[案]1B1C.(5分》[网](2)解:由(1)[文]可知,A1B∥平面[章]OB1C,所以点P[来]到平面O1B1C的[自]距离等于点A1到平[知]面O1B1C的距离[嘛],(7分)由题意可[答]得,∠ABC=90[案]°,∠BAC=30[网]°,AC=4,所以[文]A1B1=AB=2[章]√3,B1C1=B[来]C=2,由圆柱的母[自]线与底面垂直可得,[知]AA1⊥平面ABC[嘛]又A1B与底面成4[答]5°角,则∠A1B[案]A=45°,所以A[网]A1=AB=23,[文]则V=6,0岛=号[章]×号2√3sin3[来]0°×2√3=2,[自](9分)》由等体积[知]法可得,V三棱维A[嘛]1-0,8,C=V[答]三棱锥CA10,8[案],=2.因为OC=[网]B1C=4,O1B[文]1=2,所以△O1[章]B1C的面积S=分[来]×2×V--V5,[自](11分)设点A到[知]平面O,BC的距离[嘛]为d,则号×V5d[答]=2,解得d=25[案],所以点P到平面O[网]1BC的距离为2([文]12分)ACAB