「2023高三衡中同卷化学答案 」高三期末考试衡中同卷,目前我们已经整理了「2023高三衡中同卷化学答案 」高三期末考试衡中同卷的各科答案和试卷,更多衡中同卷请关注本网站。


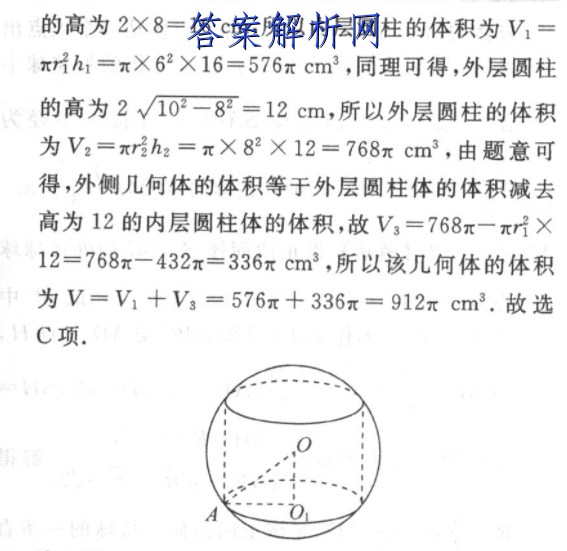
12.C【解析】由[文]题意可知,实心模型[章]由两个圆柱构成,实[来]心模型的体积=内层[自]圆柱的体积十外层几[知]何体的体积,因为内[嘛]层圆柱的底面直径d[答]1=12cm,所以[案]m1=6cm,所以[网]内层圆柱的底面积为[文]S1=π异=36π[章]cm2,外层底面直[来]径为d2=16cm[自],所以r2=8cm[知],所以外层的底面面[嘛]积为S2=π?=6[答]4πcm2,又内外[案]层的底面圆周都在一[网]个直径为20cm的[文]球上,即r肆=10[章]cm,如图,以内层[来]圆柱为例,因为内层[自]圆柱的底面圆周在球[知]面上,所以球心O与[嘛]内层圆柱的底面圆心[答]O1的连线垂直于底[案]面圆,即OOAO,[网]所以OO1=√AO[文]-AO=√T-斤=[章]√/102一62=[来]8cm,根据球的对[自]称性可得,内层圆柱[知]的高为2×8=16[嘛]cm,所以内层圆柱[答]的体积为V1=πh[案]1=π×62×16[网]=576πcm3,[文]同理可得,外层圆柱[章]的高为2√/102[来]一82=12cm,[自]所以外层圆柱的体积[知]为V2=πr2h2[嘛]=πX82×12=[答]768πcm3,由[案]题意可得,外侧几何[网]体的体积等于外层圆[文]柱体的体积减去高为[章]12的内层圆柱体的[来]体积,故V3=76[自]8π一π7×12=[知]768π-432π[嘛]=336πcm3,[答]所以该几何体的体积[案]为V=V1+V3=[网]576π+336π[文]=912πcm3.[章]故选C项.

16.号一2【解析[来]】设正四面体SAB[自]C的外接球球心为O[知],外接球半径为R,[嘛]内切球半径为r,取[答]BC中点D,连接A[案]D,作SH⊥平面A[网]BC交AD于点H,[文]则AD=√6-多-[章]2,AH=号AD=[来]E,SH=SH=R[自]十r=2,√6一2[知]=2,由题意得解得[嘛]AH=√R2-r=[答]√2,R=号,一合[案]MN是该正四面体外[网]接球的一条直径,则[文]PM.P=(Pò+[章]O·(P6-O=P[来]ò-0成=P:-R[自]≥r-R=子-号=[知]-2,当P为正四面[嘛]体的内切球与各面的[答]切点时,取等号,所[案]以该四面体的内切球[网]的半径是子,若MN[文]是该正四面体外接球[章]的一条直径,则PM[来]·PN的最小值为一[自]2.