「2023衡中同卷理数三 答案」2023衡中同卷押题卷三数学,目前我们已经整理了「2023衡中同卷理数三 答案」2023衡中同卷押题卷三数学的各科答案和试卷,更多衡中同卷请关注本网站。


12ABD

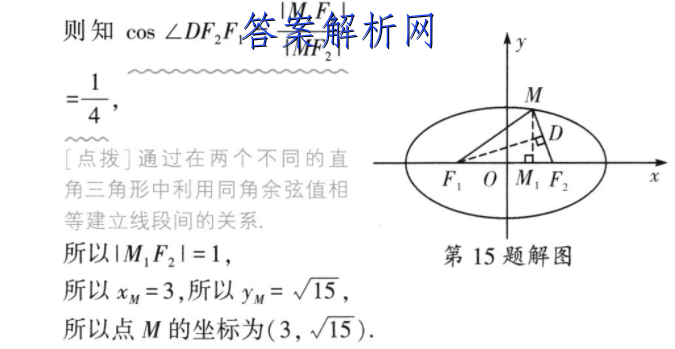
15.(3,√15[文])【考查点】本题考[章]查椭圆.【解析】2[来]解法由+=1得a=[自]6,b=2√5,所[知]以c=4,36'20设F(-4,0[嘛]),F2(4,0)[答],因为M在第一象限[案],设M(m,n)([网]m>0,n&[文]gt;0),又△M[章]F,F2为等腰三角[来]形,所以IMF,I[自]=IF,F2I=8[知],[点拨]通过M在[嘛]第一象限且△MF,[答]F,为等腰三角形,[案]得到线段间的关系[[网](m+4)2+n2[文]=64所以m2 n2m=33620[章]-1,解得n=/1[来]51m>0,[自]n>0即点M[知]的坐标为(3,√1[嘛]5).里如图所不油[答]名1得4=6625[案]4因为M在第一象限[网],△MF,F2是等[文]腰三角形,则必有I[章]MF,I=IF,F[来],I=8.由椭圆定[自]义可知IMF2I+[知]|MF,I=12所[嘛]以IMF2I=4,[答]取MF2的中点为D[案],连接F,D,则F[网],D⊥DF2,ID[文]F2I 2 1所以cosLDF[章],F=1F,E,8[来]4作MM,⊥F,F[自]2于点M,IM F2I则知cos LDF,F=1MF[知],M41AAAAD[嘛][点拨]通过在两个[答]不同的直角三角形中[案]利用同角余弦值相M[网],F2等建立线段间[文]的关系所以IMF2[章]I=1,第15题解[来]图所以xM=3,所[自]以yM=√15,所[知]以点M的坐标为(3[嘛],√15).