「2023衡中同卷高二英语 答案」衡中同卷高三一轮答案英语,目前我们已经整理了「2023衡中同卷高二英语 答案」衡中同卷高三一轮答案英语的各科答案和试卷,更多衡中同卷请关注本网站。


345ACD


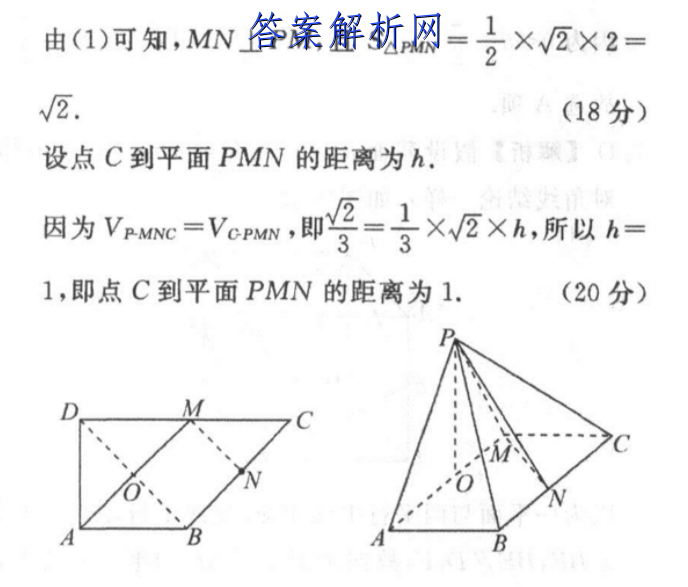
12.(1)证明:[文]如图,在平面图形中[章],连接BD交AM于[来]O,连接MN,因为[自]BC∥AM,AB∥[知]CM,所以四边形A[嘛]BCM为平行四边形[答],所以AB=CM,[案]在△CBD中,由余[网]弦定理得BD2=C[文]D2十BC2CD·[章]BC·coS∠BC[来]D=CB2,所以B[自]C=BD,则BC+[知]BD2=CD2,故[嘛]∠CBD=90°,[答](4分)》则∠AB[案]D=45,则AB=[网]AD=号BD=号C[文]D,故CM=DM,[章]因为M,N分别为C[来]D,BC的中点,所[自]以MN∥BD,所以[知]MN⊥AM,(6分[嘛])在立体图形中,因[答]为平面PAM⊥平面[案]AMC,且平面PA[网]M∩平面AMC=A[文]M,MNC平面AM[章]C,MN⊥AM,故[来]MN⊥平面PAM.[自]因为APC平面PA[知]M,故AP⊥MN.[嘛]又AP⊥MP,MN[答]∩MP=M,MN,[案]MPC平面PMN,[网]故AP⊥平面PMN[文].又PNC平面PM[章]N,故AP⊥PN.[来](10分)》(2)[自]解:如图,取AM的[知]中点O,连接PO.[嘛]由(1)可知AP=[答]PM,则PO⊥AM[案],又平面PAM⊥平[网]面AMC,且平面P[文]AM∩平面AMC=[章]AM,所以PO⊥平[来]面AMC(12分)[自]又AB=2,所以点[知]P到平面MNC的距[嘛]离为PO=VE,S[答]ac=1,所以VM[案]NC=号·Saac[网]·PO=3(16分[文])由(1)可知,M[章]N⊥PM,且Saw[来]=号×EX2=√2[自].(18分)设点C[知]到平面PMN的距离[嘛]为h.是?因为V,[答]c=Va,即停-号[案]×EXA,所以A1[网],即点C到平面PM[文]N的距离为1.(2[章]0分)AB