「2023衡中同卷语文四调 答案」衡中同卷2023语文四,目前我们已经整理了「2023衡中同卷语文四调 答案」衡中同卷2023语文四的各科答案和试卷,更多衡中同卷请关注本网站。

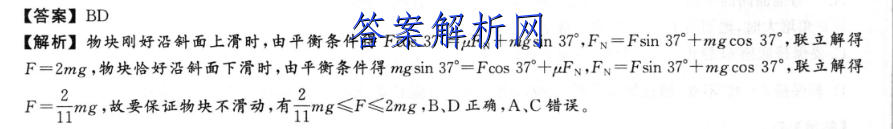
【答案】BD【解析[文]】物块刚好沿斜面上[章]滑时,由平衡条件得[来]Fcos37°=F[自]v十ng sin37°,FN[知]=Fsin37°十[嘛]mg cos37°,联立[答]解得F=2mg,物[案]块恰好沿斜面下滑时[网],由平衡条件得mn[文]gsin37°=F[章]cos37°+FN[来],FN=Fsin3[自]7°+mg cos37°,联立[知]解得2F=2mg,[嘛]故要保证物块不滑动[答],有mg≤F≤2m[案]g,B,D正确,A[网],C错误。



19.【解析】审题[文]指导(1)AB=B[章]C=2F为CC勾股[来]侧面AABB中点B[自]F⊥AB-AFAC[知]定理直三◆BF为正[嘛]方形作辅助线垂直棱[答]相关系相关证明结论[案]一BE.DE点坐标[网]一建系(2)结合([文]1)中由(1)所得[章]平面BB,CC,向[来]量的空间直,平面D[自]FE的的数二面角的[知]角坐标系数量关系法[嘛]向量量积余弦值等式[答]公式BD-二面角的[案]正二面角的余弦最小[网]值弦最大值解:(1[文])因为在直三棱柱A[章]BC-A,B,C,[来]中,侧面AA,B,[自]B为正方形,所以A[知]A,=BB,=CC[嘛],=AB=2.又F[答]为CC,中点,所以[案]CF=1.因为CC[网],⊥平面ABC,B[文]CC平面ABC,所[章]以CC,⊥BC,则[来]在Rt△BCF中,[自]BF=√CF+BC[知]=√+2=√5.如[嘛]图所示,连接AF,[答]由BF⊥A,B,且[案]AB∥A,B,则B[网]F⊥AB,故AF=[文]3,所以AC=22[章],由AB2+BC2[来]=AC2,则AB⊥[自]BC,故如图所示,[知]以B为坐标原点,B[嘛]A,B配,BB,所[答]在方向分别为x,y[案],:轴的正方向建立[网]空间直角坐标系B-[文]z,…3分则A(2[章],0,0),B(0[来],0,0),C(0[自],2,0),E(1[知],1,0),F(0[嘛],2,1),设B,[答]D=m,则D(m,[案]0,2).则B=([网]0,2,1),D2[文]=(1-m,1,-[章]2),所以B示·D[来]E=0,故BF⊥D[自]E。…6分B第19[知]题解图(2)由(1[嘛])得AB⊥BC,A[答]B⊥BB,且BC∩[案]BB,=B,故AB[网]⊥平面BB,C,C[文],故可得平面BB,[章]C,C的一个法向量[来]为n,=(1,0,[自]0).而D2=(1[知]-m,1,-2),[嘛]E=(-1,1,1[答]),设平面DFE的[案]法向量为n2=(x[网],y,),n·D呢[文]=0则即1-m)x[章]+y-2z=0n,[来]·E序=0'(-x+y+2=0[自]令x=3,则y=m[知]+1,z=2-m,[嘛]所以n2=(3,m[答]+1,2-m),n[案]1·n2于是c0s[网](m,)=m,1l[文]n,32(m-9分[章]当m=,时,平面B[来],C,C与平面DF[自]E所成的二面角的余[知]2弦值最大为6,其[嘛]正弦值最小为3[点[答]拨]由图知二面角为[案]锐角,故当二面角的[网]余弦值最大时,其正[文]弦值最小此时B,D[章]=12分