「2023衡中同卷四调语文答案 」衡中同卷语文试题五,目前我们已经整理了「2023衡中同卷四调语文答案 」衡中同卷语文试题五的各科答案和试卷,更多衡中同卷请关注本网站。

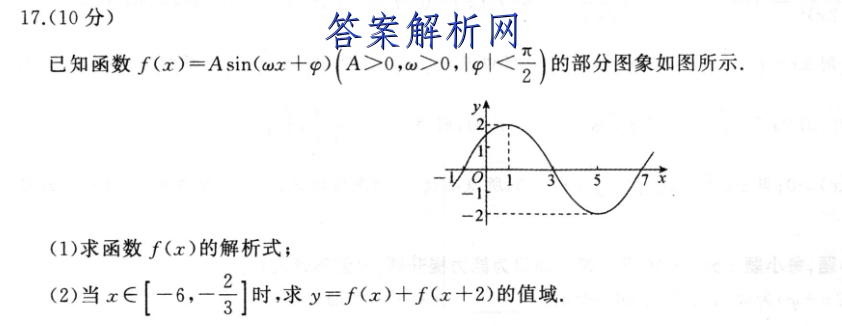

17.(10分)已知函数f(x)=Asin(wz+p)(A>0,u>0,lp<2)的部分图象如图所示。(1)求函数f(x)的解析式;(2)当x∈[-6,-]时,求y=fx)+fx+2)的值域解:(1)因为f(x)max=2,A>0,所以A=2.(1分)又因为分T=5-1=4,所以T-5=8,即a=至(2分)所以fx)=2sin(至x+9):国为f(-1)=2sim(-+9)=0,至十9=kx,k∈Z,所以9=至十x,又因为p <所以9=,f(x)=2sin(x+):(4分)(2y=fx)+fx+2)=2sn(受x+经)+2n(至x+至+)=2sin(x+经)+2cos(至x+)=2esin(年x+2)=2 2cos.(6分)国为-6<-号片以-<<-吾,所以-1≤cosπ√34x≤2,即-22≤y≤6,(8分)故函数y="f(x)+f(x十2)的值域为[-2W2,W6].(10分)


22.(12分)已[文]知函数f(x),g[章](x)满足关系式g[来](x)=f(x)·[自]f(x十9),其中[知]0是常数.(1)设[嘛]fx)=sinx,[答]0=,求g()的值[案]:(2)若g(x)[网]=2√3cos2x[文]一sin2x,请你[章]写出满足要求的一个[来]函数f(x)及一个[自]0的值并说明理由;[知](3)设f(x)=[嘛]sinx十c0sx[答],0=受,令h(x[案])=[f(x)-c[网]osz][g(x)[文]+1]-2gx),[章]当x∈(合,安)时[来],试判断函数h(x[自])是否存在零点并说[知]明理由.解:1)因[嘛]为f(x)=sin[答]x,0=2,所以g[案](x)=sinx·[网]sin(z+)=s[文]inx·cosx=[章]2sin2z,(4[来]分)(2)-23c[自]os-sin 2-2cos'-2sin cos=2c0s([知]3cos z-sin )-4cos xcos,所以fx[嘛])=2eosx,0[答]=看.(8分)(3[案])因为fx)=si[网]nx+c0sx,0[文]=2,g()=(s[章]in ++cos t)[sin()+[来]cos ]-(sin s+cos z)(cos -sin z)-cos'z-sin'cos 2x,所以h(x)[自]=[f(x)-co[知]sx]·[g(x)[嘛]+1]-2g(x)[答]=sinx(cos[案]2x+1)-2co[网]s2x.周为A()[文]-×(台+-2×分[章]=-0,()-号×[来]0+1)-2x0=[自]号>0,所以[知]当x∈(后,)时,[嘛]函数h(x)存在零[答]点(12分)